Reading Qs - Derivatives of Polynomials (Homework)

March 03, 2022 Post a Comment

Evidence General Find Show Mobile Find Show All NotesHide All Notes

Full general Discover

Surprise update today. I was going to hold off on this for a few weeks while I worked on a couple of other things just decided to become ahead and button a couple of changes to the website today as the remainder of the changes were all behind the scenes, so to speak, and shouldn't (fingers crossed) have an impact on the site or people using it.

Beginning, and nigh noticeable, is a change to a "fixed width" content area simply to make the website a little more than "consistent" on about desktop/laptop monitors. I as well added a little space between lines of text. Hopefully these changes will make the site a little easier to read. Note that you may demand to clear your browser enshroud to go this alter to display right away.

Adjacent, for a variety of reasons I have stopped offer pdf downloads of individual sections and chapters for those using that feature. Without going into keen detail on the decision I am making a change to the "source" documents that will brand generating chapter/department pdf's much more difficult while at the same time making it easier to generate the full book pdf and (hopefully) finally allow me to have "links" to other sections of the volume be active in the pdf files.

At the nowadays fourth dimension, and for the foreseeable future, any current link to a affiliate or section pdf file will not break but will redirect to download the full book pdf instead of the chapter/section file and the actual pdf files for the capacity/sections will be removed from the website.

Paul
March 1, 2022

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.east. you are probably on a mobile telephone). Due to the nature of the mathematics on this site information technology is best views in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (should be able to scroll to come across them) and some of the menu items volition be cut off due to the narrow screen width.

Department 3-two : Interpretation of the Derivative

For issues one and two use the graph of the function, \(f\left( x \right)\), judge the value of \(f'\left( a \correct)\) for the given values of \(a\).

1. \(a = - 2\)
2. \(a = 3\)
Solution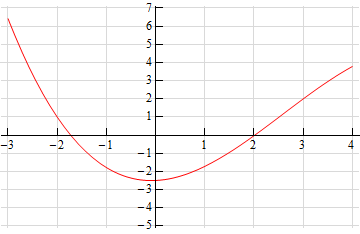
1. \(a = one\)
2. \(a = 4\)
Solution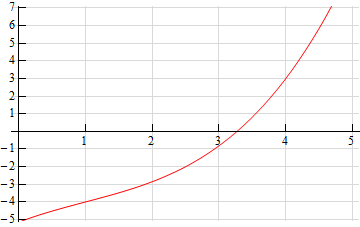

For issues three and 4 sketch the graph of a role that satisfies the given weather.

\(f\left( i \right) = three\), \(f'\left( 1 \right) = i\), \(f\left( 4 \correct) = v\), \(f'\left( 4 \right) = - 2\) Solution
\(f\left( { - 3} \right) = 5\), \(f'\left( { - 3} \right) = - 2\), \(f\left( 1 \correct) = 2\), \(f'\left( i \correct) = 0\), \(f\left( 4 \correct) = - 2\), \(f'\left( four \right) = - 3\) Solution

For problems five and 6 the graph of a office, \(f\left( ten \correct)\), is given. Use this to sketch the graph of the derivative, \(f'\left( x \right)\).

Solution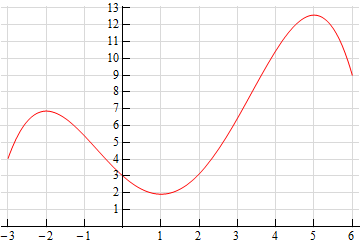
Solution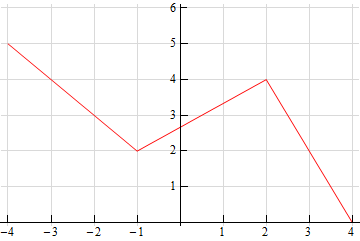
Answer the post-obit questions about the office \(W\left( z \right) = 4{z^two} - 9z\).
1. Is the function increasing or decreasing at \(z = - 1\)?
2. Is the office increasing or decreasing at \(z = 2\)?
3. Does the role ever cease changing? If yes, at what value(s) of \(z\) does the part cease irresolute?
Solution
What is the equation of the tangent line to \(f\left( ten \right) = 3 - 14x\) at \(x = eight\). Solution
The position of an object at whatever fourth dimension \(t\) is given by \(\displaystyle due south\left( t \right) = \frac{{t + 1}}{{t + iv}}\).
1. Determine the velocity of the object at any time \(t\).
2. Does the object ever stop moving? If yes, at what time(south) does the object end moving?
Solution
What is the equation of the tangent line to \(\displaystyle f\left( x \right) = \frac{5}{x}\) at \(\displaystyle x = \frac{one}{two}\)? Solution
Determine where, if anywhere, the function \(thousand\left( ten \right) = {ten^3} - two{x^2} + x - 1\) stops changing. Solution
Determine if the function \(Z\left( t \right) = \sqrt {3t - four} \) increasing or decreasing at the given points.
1. \(t = 5\)
2. \(t = 10\)
3. \(t = 300\)
Solution
Suppose that the volume of h2o in a tank for\(0 \le t \le 6\) is given by \(Q\left( t \right) = 10 + 5t - {t^two}\).
1. Is the volume of h2o increasing or decreasing at \(t = 0\)?
2. Is the volume of water increasing or decreasing at \(t = 6\)?
3. Does the volume of water ever cease irresolute? If yes, at what times(s) does the volume stop changing?
Solution